Empty Blog

Normalizing Flows (NFs) are generative models that keep every layer invertible. They learn a mapping (f: x \rightarrow z) that pushes complex data (x) into a simple base distribution (p(z)) (usually a standard Gaussian), and the inverse (f^{-1}) serves as a sampler. Because (f) is invertible, we get an exact likelihood via the change-of-variables formula:

[ \log p(x) = \log p(z) + \log \left|\det \frac{\partial f(x)}{\partial x}\right|. ]

That determinant term is the “cost of twisting space,” so the art of NFs is designing layers where the Jacobian determinant is cheap to compute but the transformation is expressive.

A quick timeline (beginner-friendly)

• NICE (2015): Additive coupling layers; determinant becomes 1, so likelihoods are trivial to compute.
• RealNVP (2016): Affine couplings and multi-scale structure; greater expressiveness while keeping determinants easy.
• Glow (2018): Invertible (1 \times 1) convolutions to mix channels, leading to sharper image synthesis.
• Beyond 2018: Spline flows, continuous-time flows (FFJORD), and flows for audio, text, and 3D.

Why use flows?

• Exact likelihoods: Unlike GANs, you can compute (\log p(x)) directly, which stabilizes training and evaluation.
• Two-way mapping: The same model handles inference (data (\rightarrow) latent) and sampling (latent (\rightarrow) data).
• Modularity: Coupling layers, permutations, and invertible convolutions can be stacked like Lego bricks.

Design knobs that matter

• Base distribution: Typically (\mathcal{N}(0, I)); richer priors can encode domain bias.
• Coupling transform: Additive/affine vs. spline-based vs. neural ODE flows—trading off flexibility and compute.
• Dimensionality handling: Squeezing, channel mixing, and multi-scale splits balance detail and efficiency.

Challenges and trends

• Scaling to long sequences and video: Determinants and inverses must stay cheap as dimensionality grows.
• Hybrid models: Combining flows with diffusion or autoregressive priors to get both likelihoods and strong samples.
• Physics- and geometry-aware flows: Injecting structure for scientific and 3D domains.

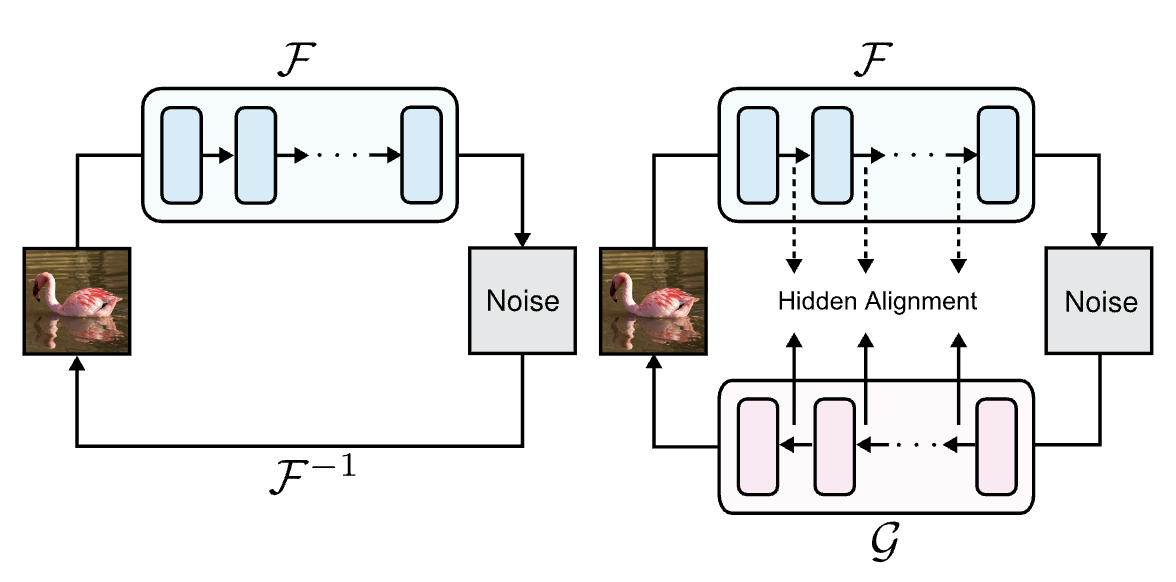
My angle (BiFlow)

In Bidirectional Normalizing Flow (BiFlow), we push for better forward–inverse symmetry: keeping invertibility while improving expressiveness in both directions. The goal is to retain exact likelihoods and efficient sampling, but make the learned map robust for high-dimensional data and downstream tasks. This direction aims to make flows practical for modern generative workloads rather than only small or toy datasets.