基本概念
设△ABC中,∠ACB=90°,则有:
sinA=ca,cosA=cb,tanA=ba,cotA=ab,secA=bc,cscA=ac。
三角函数常用值

三角函数基本关系
sin2α+cos2α=1
tan2α+1=sec2α
cot2α+1=csc2α
sinα=tanα∗cosα
cosα=cotα∗sinα
tanα=sinα∗secα
cotα=cosα∗cscα
secα=tanα∗cscα
cscα=secα∗cotα
tanα∗cotα=1
sinα∗cscα=1
cosα∗secα=1
和差公式
cos(α+β)=cosα⋅cosβ−sinα⋅sinβ
cos(α−β)=cosα⋅cosβ+sinα⋅sinβ
sin(α±β)=sinα⋅cosβ±cosα⋅sinβ
tan(α+β)=1−tanα⋅tanβtanα+tanβ
tan(α−β)=1+tanα⋅tanβtanα−tanβ
辅助角公式
Asinα+Bcosα=(A2+B2)1/2sin(α+t),
其中
sint=(A2+B2)1/2B,
cost=(A2+B2)1/2A
倍角与三倍角公式
sin(2α)=2sinα⋅cosα=tanα+cotα2
cos(2α)=cos2α−sin2α=2cos2α−1=1−2sin2α
tan(2α)=1−tan2α2tanα
sin(3α)=3sinα−4sin3α
cos(3α)=4cos3α−3cosα
半角公式
sin2a=±21−cosα
cos2a=±21+cosα
tan2a=±1+cosα1−cosα=1+cosαsinα=sinα1−cosα
万能公式
sinα=1+tan22a2tan2a
cosα=1+tan22a1−tan22a
tanα=1−tan22a2tan2a
诱导公式
1.
设t=2kπ,其中k是整数,则有:
sin(t+a)=sina,且对cos,tan,cot也是如此。
2.
sin(π+a)=−sina,且对cos也是如此。
tan(π+a)=tana,且对cot也是如此。
3.
sin−a=−sina,且对$ \tan ,\cot$也是如此。
cos−a=cosa
4.
cos(π−a)=−cosa,且对tan,cot也是如此。
sin(π−a)=sina
5.
sin(2π±a)=cosa
cos(2π∓a)=±sina
tan(2π∓a)=±cota
cot(2π∓a)=±tana
6.
sin(23π±a)=−cosa
cos(23π±a)=±sina
tan(23π∓a)=±cota
cot(23π∓a)=±tana
积化和差、和差化积公式
sinα⋅cosβ=2sin(α+β)+sin(α−β)
cosα⋅sinβ=2sin(α+β)−sin(α−β)
cosα⋅cosβ=2cos(α+β)+cos(α−β)
sinα⋅sinβ=2cos(α+β)−cos(α−β)
sinα+sinβ=2sin2α+βcos2α−β
sinα−sinβ=2cos2α+βsin2α−β
cosα+cosβ=2cos2α+βcos2α−β
cosα−cosβ=−2sin2α+βsin2α−β(注意!有负号!)
正余弦定理
设有△ABC,A,B,C对边分别为a,b,c。
正弦定理:sinAa=sinBb=sinCc=2R,其中R是外接圆半径。
余弦定理:a2=b2+c2−2bccosA
三角形的面积公式
S=21absinC
以下是补充:
S=21hd=4Rabc=2a+b+cr=p(p−a)(p−b)(p−c),其中:
d是底,h是高,r,R分别是△ABC的内切圆和外接圆半径,p=2a+b+c。
三角形其他公式
sin(A+B)=sinC
cos(A+B)=−cosC
tan(A+B)=−tanC
sin2A+B=sin2π−C=cos2C
tan2A+B=cot2C
三角函数的图像和一些性质
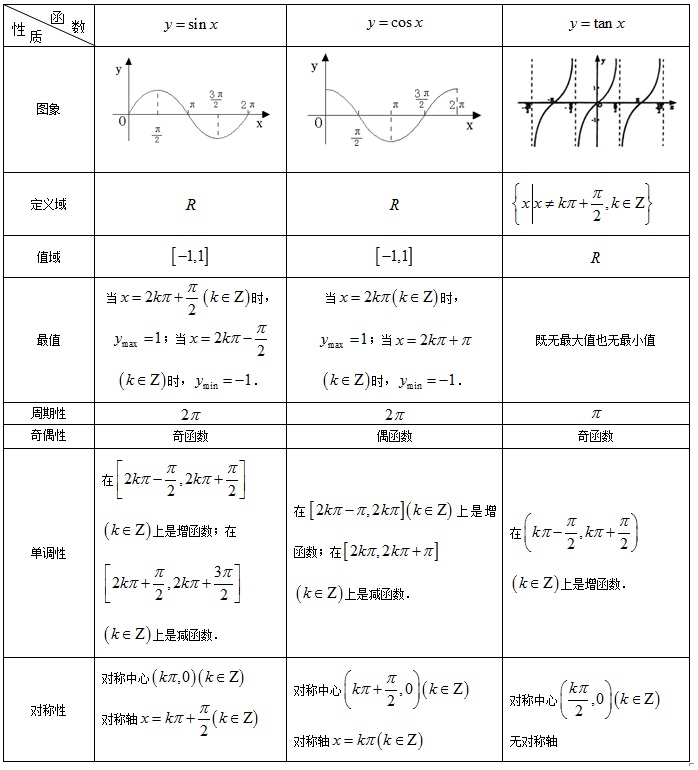
补充:
1.奇偶性
若D关于原点对称,且对于任意的x属于D,总有f(−x)=f(x),则称f(x)为偶函数。如果f(−x)=−f(x),则称f(x)为奇函数。
2.周期性
若存在常数T!=0,使得x取定义域的每一个值时,均有f(x)=f(x+T),则称f(x)是周期函数,T是它的周期。
3.单调性
设f(x)在集合S中有定义,且S属于定义域D。若对于任何两个属于B的数x1<x2,均有f(x1)<f(x2),则称f(x)在S上是增函数。
反函数则相反。
三角不等式
1)设△ABC,x,y,z是任意实数。则x2+y2+z2>=2xycosA+2yzcosB+2zxcosC。
2)∣acosx+bsinx∣<=a2+b2
反三角函数的定义
设f(x)=sinx,则f−1(x)=arcsinx。
同理,arccos,arctan的定义也可以给出。

