LCA
一 · LCA的定义
给定一颗有根树,若结点Z是X和Y的祖先,则称Z为X,Y的公共祖先。
在X,Y的公共祖先中,深度最大的一个结点Z′为X,Y的最近公共祖先,
称作LCA(Least Common Ancestors) 。
如下图,结点9,12的公共祖先有结点1,3,其中3是它们的最近公共祖先。
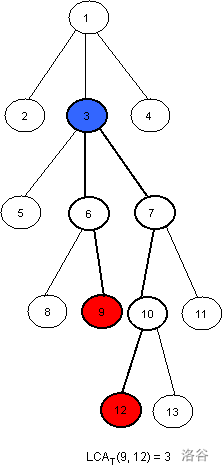
二 · 求法
1 树上倍增
1.1 f数组的定义
定义f[x][k]表示x的2k辈祖先,也就是说从x出发,向根节点走2k步到达的结点。
若结点不存在,则f[x][k]=0。
若存在,则满足f[x][k]=f[ f[x][k−1] ][ k−1 ]。因为向上跳2k步,就相当于跳两个2k−1步。
初始化f[x][0]=x的父亲。
这样的算法复杂度是O(n×logn)。
1.2 利用f数组计算LCA
设dep[u]表示u的深度,一遍dfs求得。
假设dep[x]>=dep[y]。用二进制拆分的思想,将结点x向上调整到y一样的深度。具体方法是:依次尝试向上走2log(dep[y]−dep[x]),...,21,20步,如果达到的点的深度不比dep[y]小,那么就跳。
若此时有x=y,则找到了LCA。
若否,则用二进制拆分,继续对x,y同时调整,保证深度一致且不相会。具体方法是:依次尝试将x,y向上走2logn,...,21,20步,如果跳完后x不等于y,则就跳。这样最后的结果就是x,y的父亲。
这样的算法复杂度也是O(n×logn)。故总体的复杂度也是如此。
1.3 完整代码
#include<bits/stdc++.h>
#define INF 2147483647
using namespace std;
const int N=500005,Q=21;
int n,m,s;
struct Edge{
int u,v;
int next;
}edge[N<<1];
int head[N],tot=0;
int dep[N],f[N][Q];
void add_edge(int u,int v){
tot++;
edge[tot].u=u;
edge[tot].v=v;
edge[tot].next=head[u];
head[u]=tot;
}
void dfs(int pos,int fa){
dep[pos]=dep[fa]+1;
f[pos][0]=fa;
for(int i=head[pos];i;i=edge[i].next){
if(edge[i].v==fa) continue;
dfs(edge[i].v,pos);
}
}
int lca(int x,int y){
if(dep[x]<dep[y]) swap(x,y);
for(int i=Q-1;i>=0;i--){
if(dep[f[x][i]]>=dep[y]){
x=f[x][i];
}
}
if(x==y) return x;
for(int i=Q-1;i>=0;i--){
if(f[x][i]!=f[y][i]){
x=f[x][i];
y=f[y][i];
}
}
return f[x][0];
}
int main(){
scanf("%d%d%d",&n,&m,&s);
for(int i=1;i<n;i++){
int u,v;
scanf("%d%d",&u,&v);
add_edge(u,v);
add_edge(v,u);
}
dfs(s,0);
for(int i=1;i<Q;i++){
for(int j=1;j<=n;j++){
f[j][i]=f[f[j][i-1]][i-1];
}
}
for(int i=1;i<=m;i++){
int u,v;
scanf("%d%d",&u,&v);
printf("%d\n",lca(u,v));
}
exit(0);
}
2 ST表
2.1 什么是ST表
引入例题:(RMQ问题)给定N个数,M次询问,每次询问给定区间[L,R],求区间内数的最大值。其中,N<=105,M<=107。
分析:如果N,M较小的话,我们可以用O(n2)的效率进行暴力。但是这里的N<=105,所以n2会超时。
然而,即使我们用logn的效率求每次的询问,我们仍然会超时。那怎么办?我们只能用O(1)求每次的询问,最多O(nlogn)效率预处理。
什么东西是logn的效率?二进制啊!
设f[i][j]表示从i到i+2j−1位置所有数的最大值。那么预处理的方程就是f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]。
对于查询,我们就可以令M=log2(R−L+1),则区间[L,R]中的最大值就是max(f[L][M],f[R-(1<<M)+1][M])。
到这里,基本上问题已经解决了。但是求log其实也是O(logn)的效率,所以需要预处理一下,也就是说lg[i]=lg[i/2]+1。
完整代码(P3865 【模版】ST表):
#include<bits/stdc++.h>
using namespace std;
const int N=100005,Q=21;
int f[N][Q],n,m,l,r;
int lg[N];
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&f[i][0]);
for(int i=1;i<=n;i++) lg[i]=lg[i/2]+1;
for(int j=1;j<Q;j++)
for(int i=1;i<=n-(1<<j)+1;i++)
f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
for(int i=1;i<=m;i++){
scanf("%d%d",&l,&r);
int mmm=lg[r-l+1];
printf("%d\n",max(f[l][mmm],f[r-(1<<mmm)+1][mmm]));
}
return 0;
}
2.2 利用ST表解决LCA问题
上面讲了那么多,那么如何用ST表解决问题呢?
我们需要做到的是,将两个点定位以后,它们中间所有点就是我们要用ST表求的点。这些点应该是两个点的LCA之下的点。如何做到这一点?用dfs序啊!
考虑一个树的dfs序列。比如下图,它的dfs序是0,1,3,1,4,1,0,2。

对于每个结点,其第一次在dfs序中出现的位置为fir[i]。则fir[L]和fir[R]之间的所有点都是LCA(L,R)和其子结点。只需在这段区间里求出深度最小值即可。这就是ST表的事情了。
需要注意的是,这个算法的常数略大,需要进行读入优化和吸氧。
2.3 完整代码
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int n,m,s;
int dfn[1000005];
//dfn[]表示树的dfs序
int dep[500005];
//dep[]表示每个结点的深度
int uu[1000005],vv[1000005],nxt[1000005];
int head[500005],tot=0;
int fir[500005],st[1000005][20];
//fir[]表示每个结点第一次出现在dfs序中的位置
//st[][]是dep[dfn[]]的st表,这里是记录最大结点
int read(){//读入优化
int x=0;
int flag=0;
char ch;
ch=getchar();
if(ch=='-') flag=1;
while(ch<'0'||ch>'9') ch=getchar();
while(ch>='0'&&ch<='9'){
x=x*10+ch-'0';
ch=getchar();
}
if(flag) x=-x;
return x;
}
void add_edge(int u,int v){
tot++;
uu[tot]=u;
vv[tot]=v;
nxt[tot]=head[u];
head[u]=tot;
}
void dfs_depth(int pos,int depth,int fa){
dep[pos]=depth;
for(int i=head[pos];i;i=nxt[i]){
if(vv[i]==fa) continue;
dfs_depth(vv[i],depth+1,pos);
}
return ;
}
void dfs(int pos,int fa){
dfn[++tot]=pos;
st[tot][0]=tot;
if(!fir[pos]) fir[pos]=tot;
for(int i=head[pos];i;i=nxt[i]){
if(vv[i]==fa) continue;
dfs(vv[i],pos);
dfn[++tot]=pos;
st[tot][0]=tot;
}
return ;
}
int main(){
n=read();
m=read();
s=read();
for(int i=1;i<n;i++){
int u,v;
u=read();
v=read();
add_edge(u,v);
add_edge(v,u);
}
dfs_depth(s,1,0);
tot=0;dfs(s,0);
for(int j=1;j<21;j++){
for(int i=1;i<=tot-(1<<j)+1;i++){
if(dep[dfn[st[i][j-1]]]<dep[dfn[st[i+(1<<(j-1))][j-1]]]){
st[i][j]=st[i][j-1];
}
else{
st[i][j]=st[i+(1<<(j-1))][j-1];
}
}
}
for(int i=1;i<=m;i++){
int u,v;
u=read();
v=read();
int l1=fir[u];
int r1=fir[v];
if(l1>r1) swap(l1,r1);
int mmm=log2(r1-l1+1);
if(dep[dfn[st[l1][mmm]]]<dep[dfn[st[r1-(1<<mmm)+1][mmm]]])
printf("%d\n",dfn[st[l1][mmm]]);
else
printf("%d\n",dfn[st[r1-(1<<mmm)+1][mmm]]);
}
exit(0);
}
Stay hungry, stay foolish.